Η απάντηση είναι ότι πιθανότατα υπάρχει, αλλά θα χρειαστεί να κάνουμε αρκετή ανάλυση στα δεδομένα του GPS. Πριν πάρουμε τα βουνά προς αναζήτηση της "βαρυτικής ανηφόρας", θα κάνουμε ένα αντίστοιχο πείραμα σε ένα δρόμο της γειτονιάς για να δούμε αν η μέθοδός μας δουλεύει. To τμήμα του δρόμου που θα ελέγξουμε ξεκινά από ένα σημείο Α και καταλήγει σε ένα σημείο Β τα οποία απέχουν μεταξύ τους 215 μέτρα. Ξέρουμε ότι το σημείο Β είναι υψομετρικά ψηλότερα (περίπου 4-5 μέτρα). Θα μπορέσουμε με μια κατάλληλη επεξεργασία του σήματος του GPS να το διαπιστώσουμε και πειραματικά;
Ξεκινάμε λοιπόν, με το GPS στο χέρι, να διανύουμε την απόσταση από το ένα σημείο στο άλλο πολλές φορές. Κατά τη διάρκεια της διαδρομής μας καταγράφουμε με το GPS τη θέση (γεωγραφικό πλάτος φ και γεωγραφικό μήκος λ) και το υψόμετρο. Σε όλο το μήκος της διαδρομής η λήψη του σήματος είναι πολύ καλή και ο δέκτης έχει τη μέγιστή του ακρίβεια. Αφού διανύσουμε την απόσταση Α-Β 15 φορές, "κατεβάζουμε" τα δεδομένα του GPS και κάνουμε αρχικά δύο γραφικές παραστάσεις: της απόστασης από το σημείο Α και του υψομέτρου, οι οποίες φαίνονται στα παρακάτω σχήματα.
Τεχνικές λεπτομέρειες: η πρώτη γραφική παράσταση, στον κατακόρυφο άξονα δεν έχει ακριβώς την απόσταση αλλά ένα μέτρο αυτής, συγκεκριμένα το άθροισμα των τετραγώνων των διαφορών γεωγραφικού μήκους και πλάτους από το σημείο Α. Επίσης στον οριζόντιο άξονα δεν είναι ο χρόνος αλλά ο αριθμός της μέτρησης.
Με βάση αυτά που διαπιστώσαμε στην προηγούμενη ανάρτηση, τα αποτελέσματα δε μας εκπλήσσουν. Η πρώτη γραφική παράσταση παρουσιάζει ταλαντωτική συμπεριφορά με πολύ λίγες διακυμάνσεις, καθώς η διανυόμενη απόσταση (~215 μέτρα) είναι πολύ μεγαλύτερη από την ακρίβεια της συσκευής (~4-5 μέτρα). Η δεύτερη γραφική παράσταση μοιάζει σε πρώτη ανάγνωση απογοητευτική. Κανονικά θα περιμέναμε να παρουσιάζει κι εκείνη μια ταλαντωτική συμπεριφορά απόλυτα συσχετισμένη με εκείνη της πρώτης. Αυτή η ταλαντωτική συμπεριφορά υπάρχει αλλά είναι κρυμμένη πίσω από ένα υπόβαθρο μεγάλων μεταβολών της καταγραφής του υψομέτρου σαν κι εκείνο που είδαμε στην προηγούμενη ανάρτηση. Το ζήτημα επομένως ανάγεται στο εξής: μπορούμε με κάποιον τρόπο να δούμε την ταλάντωση που είναι κρυμμένη πίσω από το υπόβαθρο των μετρήσεων του υψομέτρου και να τη συσχετίσουμε με την ταλάντωση της θέσης;
Υπάρχουν δύο διαδικασίες επεξεργασίας για να αποκαλύψουμε αυτή την ταλάντωση, η πρώτη είναι πιο απλή και εύκολη υπολογιστικά ενώ η δεύτερη απαιτεί κάποιους περισσότερους υπολογισμούς.
Διαδικασία 1: ομαλοποίηση (smoothing) της καμπύλης του υψομέτρου
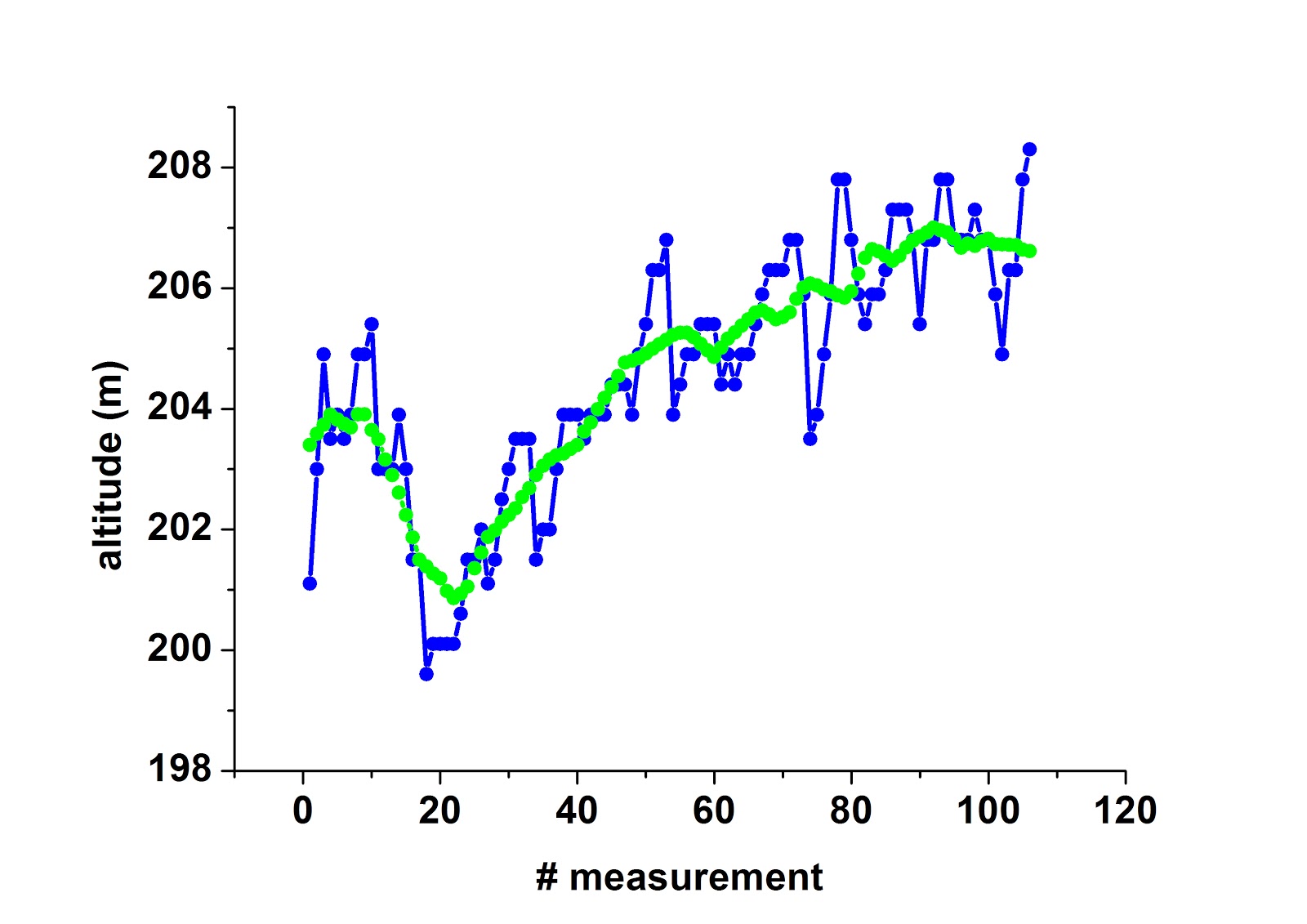
Για να προσεγγίσουμε το υπόβαθρο το οποίο μας κρύβει την ταλάντωση, μπορούμε να υποθέσουμε πως αυτό ακολουθεί κατά κάποιο τρόπο τη μέση τιμή της καμπύλης. Κάνουμε λοιπόν ομαλοποίηση (smoothing) της καμπύλης λαμβάνοντας για κάθε σημείο, τη μέση τιμή που δίνουν τα γειτονικά του σημεία. Το αποτέλεσμα της ομαλοποίησης φαίνεται στο ακόλουθο σχήμα (πράσινη καμπύλη).
Υποθέτοντας ότι το υπόβαθρο είναι η πράσινη (ομαλοποιημένη) καμπύλη, η ταλάντωση κρύβεται στη διαφορά μεταξύ των μετρήσεων υψομέτρου (μπλέ καμπύλη) και στο υπόβαθρο (πράσινη καμπύλη). Η διαφορά αυτή φαίνεται στο ακόλουθο σχήμα (με h συμβολίζουμε το υψόμετρο και με hB το υπόβαθρο).
Υπάρχει μια ταλαντωτική συμπεριφορά που δεν παρουσιάζει την ομαλότητα της καμπύλης της απόστασης αλλά ας προσπαθήσουμε τώρα να συσχετίσουμε το μέγεθος h - hB με την απόσταση. Υπάρχουν δύο τρόποι να γίνει αυτός ο συσχετισμός:
Τρόπος 1: Υπολογισμός της κλίσης της ευθείας ελαχίστων τετραγώνων
Ο δρόμος που μελετάμε έχει σχεδόν σταθερή κλίση, επομένως η γραφική παράσταση h - hB σα συνάρτηση της απόστασης θα έπρεπε να ακολουθεί μια ευθεία. Αν η ευθεία έχει θετική κλίση τότε έχουμε ανηφόρα, αν έχει αρνητική τότε έχουμε κατηφόρα. Ας δούμε λοιπόν πως μοιάζουν τα σημεία μας στο επίπεδο όπου οριζόντιος άξονας είναι η απόσταση και κατακόρυφος η διαφορά h - hB.
Δεν πολυμοιάζουν να ακολουθούν ευθεία αλλά ας κάνουμε μια προσαρμογή μιας ευθείας με τη μέθοδο των ελαχίστων τετραγώνων. Το αποτέλεσμα μας δίνει για την κλίση της τιμή 268.02841 με σφάλμα ίσο με 127.50361. Το σφάλμα είναι μεγάλο (όπως αναμένονταν δεδομένης της διασποράς των σημείων) αλλά είναι μικρότερο από την κλίση, επομένως μπορούμε με ασφάλεια να πούμε ότι από το Α στο Β έχουμε ανηφόρα. Και πράγματι έτσι είναι: ο δρόμος που μελετήσαμε είναι και δείχνει ανηφόρα!
Τρόπος 2: Υπολογισμός του συντελεστή συσχέτισης του Pearson
Ένα μέγεθος το οποίο μπορεί να ποσοτικοποιήσει τη συσχέτιση δύο μεγεθών είναι ο συντελεστής συσχέτισης του Pearson. Αυτός είναι ένα μέτρο του κατά πόσο δύο μεταβλητές (ας τις πούμε x και y) μεταβάλλονται μαζί. Θετικός συντελεστής συσχέτισης σημαίνει ότι όσο αυξάνεται η μία μεταβλητή αυξάνεται και η άλλη. Αρνητικός συντελεστής συσχέτισης σημαίνει ότι όσο αυξάνεται η μία μεταβλητή μειώνεται η άλλη. Όσο πιο μεγάλη είναι η απόλυτη τιμή του συντελεστή συσχέτισης τόσο πιο ισχυρή είναι η συσχέτιση των δύο μεταβλητών x και y. Ο συντελεστής συσχέτισης ορίζεται από τον τύπο:
όπου το < > υποδηλώνει τη μέση τιμή. Αν η σχέση των x και y είναι γραμμική (πχ y=ax), ο συντελεστής παίρνει τη μέγιστη απόλυτη τιμή του που είναι η μονάδα: r = 1 αν a>0 και r = -1 αν a<0. Ας εξετάσουμε λοιπόν κατά πόσο είναι συσχετισμένα τα μεγέθη της απόστασης και της διαφοράς υψομέτρου h - hB. Το αποτέλεσμα είναι r = 0.2353, δηλαδή τα μεγέθη είναι θετικά συσχετισμένα: αυξάνομένης της απόστασης από το Α, αυξάνεται και το υψόμετρο. Βρήκαμε λοιπόν και πάλι ότι έχουμε ανηφόρα!
Πριν καταλήξουμε οριστικά στο συμπέρασμα ότι έχουμε ανηφόρα καλό είναι να συγκρίνουμε το συντελεστή αυτόν που υπολογίσαμε με εκείνον της συσχέτισης κάποιων άλλων μεγεθών. Έτσι, υπολογίζουμε επιπλέον τη συσχέτιση της απόστασης με δύο ακόμα μεγέθη: το υψόμετρο όπως το παίρνουμε από το GPS χωρίς κανένα μετασχηματισμό καθώς και μια τεχνητή σειρά δεδομένων που αποτελείται από τυχαίους αριθμούς. Τα αποτελέσματα είναι αντίστοιχα r = 0.07135 και r = 0.05328. Και τα δύο είναι πολύ μικρότερα από την τιμή 0.2353, κάτι που υποδηλώνει ότι η θετική συσχέτιση της απόστασης με το h - hB δεν είναι κάποιο τυχαίο γεγονός.
Διαδικασία 2: μετασχηματισμός Fourier και φιλτράρισμα συχνοτήτων
Μέσα στην καμπύλη του υψομέτρου όπως την παίρνουμε από το GPS (η μπλέ καμπύλη που είδαμε στο δεύτερο σχήμα) είναι κρυμμένη μια περιοδικότητα στη μεταβολή του υψομέτρου. Η περιοδικότητα αυτή έχει κάποια συχνότητα (ή ακριβέστερα ένα φάσμα συχνοτήτων) την οποία μπορούμε να βρούμε εύκολα κοιτώντας την καμπύλη της απόστασης (την πρώτη κόκκινη καμπύλη). Είναι φανερό ότι η καμπύλη αυτή έχει μια περιοδικότητα. Επειδή το υψόμετρο μεταβάλλεται μονότονα με την απόσταση, την ίδια περιοδικότητα θα έχει και η μεταβολή του υψομέτρου. Αυτή είναι η κρυμμένη περιοδικότητα που ψάχνουμε. Το σκεπτικό λοιπόν είναι να βρούμε το φάσμα συχνοτήτων της απόστασης και από τις συχνότητες που συναποτελούν την καμπύλη του υψομέτρου και να εστιαστούμε σε εκείνες που μας ενδιαφέρουν. Παρακάτω περιγράφουμε πιο αναλυτικά τη μέθοδο.
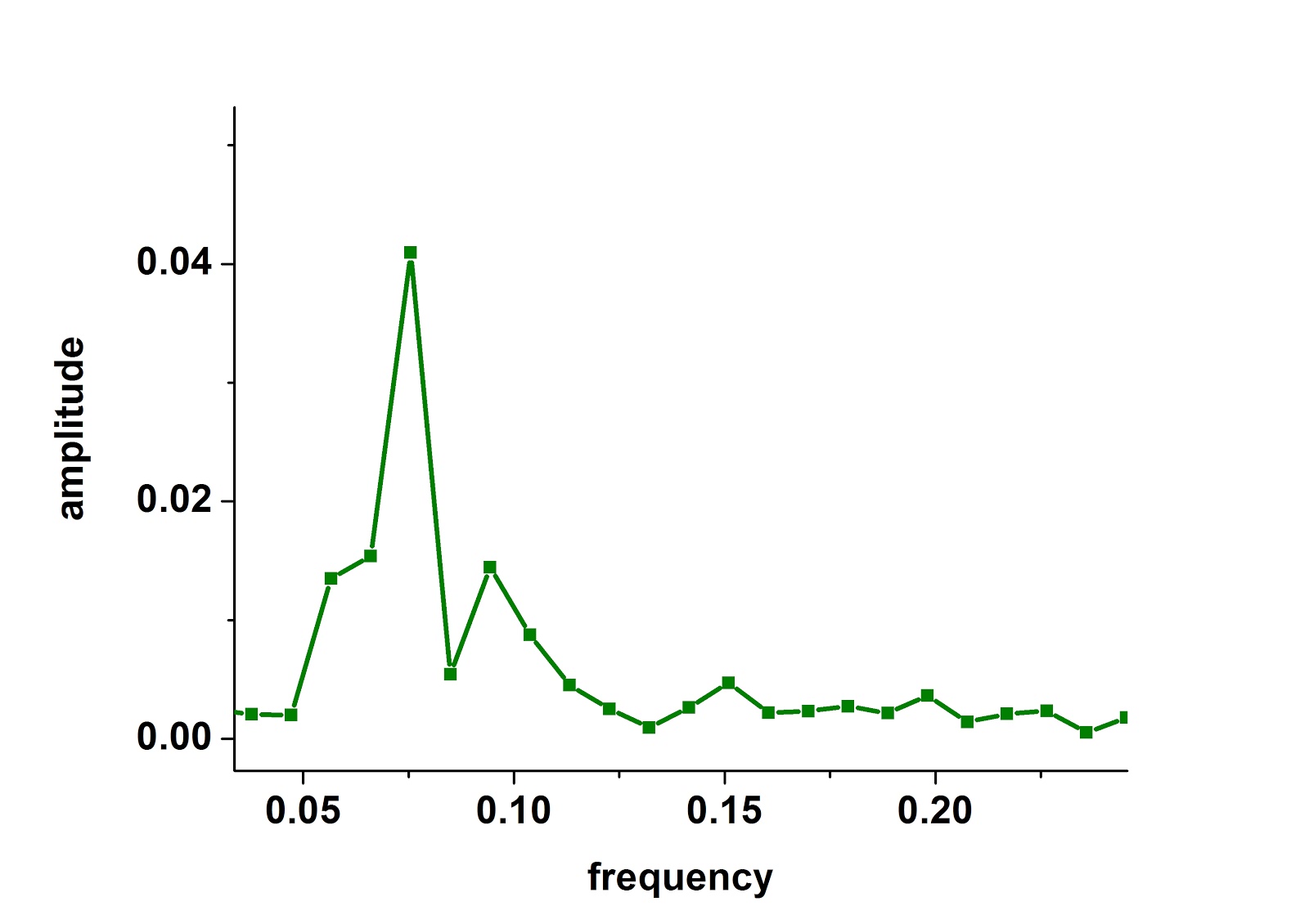
Ας συμβολίσουμε με h(t) την καμπύλη υψομέτρου που παίρνουμε από το GPS και με s(t) την αντίστοιχη καμπύλη "απόστασης" (τεχνική λεπτομέρεια: η έννοια του χρόνου t χρησιμοποιείται κάπως καταχρηστικά, καθώς όπως είπαμε στον οριζόντιο άξονα είναι ο αριθμός της μέτρησης και οι μετρήσεις δεν είναι ακριβώς ισόχρονες). Για να βούμε το φάσμα των συχνοτήτων της s(t) θα κάνουμε ένα μετασχηματισμό Fourier:
Όπως αναμένονταν από την εμφανή περιοδικότητα της s(t), το πλάτος είναι κυρίως συγκεντρωμένο σε μια περιοχή συχνοτήτων μεταξύ των τιμών f1=0.0471 και f2=0.132. Η ιδέα τώρα είναι να "κρατήσουμε" από την h(t) ότι υπάρχει μέσα σε αυτό το εύρος συχνοτήτων πετώντας όλα τα υπόλοιπα και αυτό γίνεται ως εξής:
1) Υπολογίζουμε το μετασχηματισμό Fourier της h(t):
2) Από όλες τις συχνότητες που περιέχει η H(f) κρατάμε μόνο εκείνες που βρίσκονται μεταξύ των f1 και f2. Πιθανότατα βέβαια στο διάστημα αυτό των συχνοτήτων, εκτός από την περιοδικότητα της μεταβολής του υψομέτρου, να υπάρχει και κάποιο μικρό πλάτος που οφείλεται σε μεταβολές του σήματος του GPS. Ουσιαστικά, φιλτράρουμε την H(f) και δημιουργούμε μια καινούργια H(f) που περιέχει συνεισφορές μόνο από το συγκεκριμένο διάστημα συχνοτήτων:
3) Για να βρούμε το μέρος της h(t) που αντιστοιχεί στο διάστημα αυτό των συχνοτήτων, εφαρμόζουμε τον αντίστροφο μετασχηματισμό Fourier σε αυτή την καινούργια H(f), και παίρνουμε μια συνάρτηση h1(t) που εμπεριέχει την περιοδικότητα στη μεταβολή του υψομέτρου:
Τώρα λοιπόν, θα συσχετίσουμε το παραπάνω h1(t) με το s(t) με τους δύο τρόπους που είδαμε προηγουμένως:
Υπολογίζοντας την κλίση της ευθείας ελαχίστων τετραγώνων στο επίπεδο s - h1 παίρνουμε την τιμή 246.17802 για την κλίση και την τιμή 88.70148 για το σφάλμα της. Και πάλι λοιπόν καταλήγουμε στο αληθές συμπέρασμα ότι ο δρόμος μας είναι πράγματι ανηφορικός από το Α στο Β, και μάλιστα με μικρότερο σχετικά σφάλμα για την κλίση της ευθείας. Στο παρακάτω σχήμα φαίνονται τα σημεία και η βέλτιστη ευθεία με την παραπάνω κλίση.
Μπορούμε να καταλήξουμε στο ίδιο συμπέρασμα υπολογίζοντας το συντελεστή συσχέτισης των s και h1 και το αποτέλεσμα είναι 0.2624. Τα μεγέθη s και h1 είναι επομένως συσχετισμένα: αυξανομένης της απόστασης από το Α αυξάνεται το υψόμετρο, άρα επαληθεύσαμε και πάλι ότι ο δρόμος είναι ανηφορικός από το Α στο Β.
Συμπερασματικά: Περιγράψαμε μια μέθοδο με την οποία μπορούμε να διαπιστώσουμε αν ένας δρόμος είναι ανηφορικός η κατηφορικός και την ελέγξαμε σε ένα δρόμο του οποίου γνωρίζουμε την κλίση. Η μέθοδος φάνηκε να δουλεύει και σε επόμενη ανάρτηση θα την εφαρμόσουμε σε ένα δρόμο που δεν ξέρουμε αν είναι ανηφορικός ή κατηφορικός: στη "βαρυτική ανηφόρα" της Πεντέλης.











Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου