Πειράματα με ένα GPS, μέρος ΙΙΙ: καταρρίπτοντας το μύθο της "βαρυτικής ανωμαλίας" της Πεντέλης

Όπως έγραψα και στην προηγούμενη ανάρτηση, στις πλαγιές της Πεντέλης, στο δρόμο που οδηγεί από την Παλαιά Πεντέλη στον Άγιο Πέτρο, σε υψόμετρο περίπου 700 μ υπάρχει ένας δρόμος που από την κατασκευή του στα τέλη της δεκαετίας του '70 τον ακολουθεί μια φήμη: σε κάποιο τμήμα του μήκους περίπου 250 μέτρων κι ενώ φαίνεται να είναι ανηφορικός, τα οχήματα συμπεριφέρονται ως να ήταν κατηφορικός. Την "ανωμαλία" αυτή την είχα παρατηρήσει κι εγώ πριν κάποια χρόνια ποδηλατώντας με κατεύθυνση από τη Νέα Μάκρη προς την Παλιά Πεντέλη: σε ένα σημείο -αμέσως μετά την πηγή στη θέση Πουρνάρα- ενώ ο δρόμος φαίνεται να ανηφορίζει, το ποδήλατο κέρδιζε ταχύτητα χωρίς να κάνω πετάλι. Αργότερα το παρατήρησα και στην αντίθετη κατεύθυνση (αν και με λιγότερη ένταση): ο δρόμος φαίνεται ελαφρά κατηφορικός, παρόλα αυτά όμως αν δεν κάνεις πετάλι χάνεις ταχύτητα. Αναφέρομαι συγκεκριμένα στο ποδήλατο γιατί με αυτό είναι πολύ ευκολότερο να αντιληφθεί κανείς το φαινόμενο σε σύγκριση με το αυτοκίνητο.

Με μια αναζήτηση που έκανα στο διαδίκτυο για το φαινόμενο, βρήκα ότι η ύπαρξη του αναφέρεται (και αναπαράγεται) σε πολλές ιστοσελίδες. Παρά τις πολλές αναφορές σε "βαρυτικές ανωμαλίες" και μεταφυσικά φαινόμενα, δεν υπάρχει δημοσιευμένη στο διαδίκτυο καμία εμπεριστατωμένη μελέτη που να επιβεβαιώνει ή να απορρίπτει την ύπαρξη ή μη βαρυτικής ανωμαλίας, αν και πιστεύω ότι σίγουρα έχουν υπάρξει κάποιες τέτοιες μελέτες. Ούτε καν η ακριβής θέση του φαινομένου δεν προσδιορίζεται και υποθέτω ότι οι περισσότεροι που αναφέρονται στο φαινόμενο ούτε που έχουν πατήσει ποτέ στο σημείο.

Έτσι λοιπόν, την ηλιόλουστη Κυριακή 13/1/2013, ξεκινήσαμε με το φίλο και συνοδοιπόρο Λάζαρο για τον εντοπισμό και τη μελέτη του φαινομένου. Ο Λάζαρος έβαλε το αυτοκίνητο και το ποδήλατο, ένα σπαστό Dahon, κι εγώ το GPS, ένα Garmin Dakota 10. Παρκάραμε το αυτοκίνητο στην πηγή στη θέση Πουρνάρα (λόγω Κυριακής είχε αρκετό κόσμο) και ακολουθήσαμε το δρόμο προς την Παλιά Πεντέλη. Στο σημείο που είναι η πηγή, ο δρόμος κάνει μια απότομη αριστερή στροφή. Στο τελείωμα της στροφής, αμέσως μετά την πηγή, αρχίζει το φαινόμενο: ο δρόμος φαίνεται αναμφίβολα ανηφορικός αλλά αν ξεκινήσουμε με πολύ μικρή ταχύτητα, το ποδήλατο επιταχύνει για ένα διάστημα περίπου 250 μέτρα. Μετά από αυτά τα 250 μέτρα, ο δρόμος γίνεται ανηφορικός οπότε σταδιακά χάνουμε ταχύτητα. Στην αντίστροφη διαδρομή, ο δρόμος φαίνεται κατηφορικός αλλά χρειάζεται να κάνουμε πετάλι για να διατηρήσουμε μια σταθερή ταχύτητα. Στον παρακάτω χάρτη φαίνεται η ακριβής θέση του φαινομένου. Κάνοντας κλικ εδώ μπορείτε να κατεβάσετε και το αντίστοιχο αρχείο kmz.

Κοιτώντας την διαδρομή από το σημείο στο χάρτη που σημειώνεται ως ΑΡΧΗ, βλέπουμε αυτό που φαίνεται στις παρακάτω εικόνες:

Η "βαρυτική ανηφόρα" της Πεντέλης. Φαίνεται ανηφόρα, συμπεριφέτεται ως κατηφόρα. Τί είναι τελικά;

  Στις εικόνες αυτές, και ιδιαίτερα στην πρώτη, φαίνεται να έχουμε να κάνουμε με ένα δρόμο που στην αρχή είναι ελαφρώς ανηφορικός και στη συνέχεια ανηφορίζει πιο έντονα και κάνει μια δεξιά στροφή. Αν όμως αφεθούμε χωρίς να κάνουμε πετάλι από το σημείο που πήραμε τις φωτογραφίες, αντί να σταματήσουμε, ανεβαίνουμε τον "ανήφορο" ως να ήταν κατήφορος. Το φαινόμενο αυτό έχει παρατηρηθεί από την εποχή της κατασκευής του δρόμου και έχει από πολλούς αποδίδεται σε βαρυτική ανωμαλία.

Τι εννοούμε όμως όταν λέμε βαρυτική ανωμαλία; Βαρυτική ανωμαλία έχουμε όταν λόγω μιας σημαντικής ανοιμοιομορφίας της κατανομής της μάζας στο εσωτερικό της γης, η επιτάχυνση της βαρύτητας έχει σημαντικά διαφορετικό μέτρο ή/και κατεύθυνση από εκείνα που προβλέπονται για τη συγκεκριμένη περιοχή. Η ύπαρξη μιας βαρυτικής ανωμαλίας στην περιοχή (πχ λόγω της ύπαρξης κάποιου πολύ μεγάλου κενού στο εσωτερικό της γης) θα είχε ως αποτέλεσμα η το διάνυσμα της επιτάχυνσης της βαρύτητας να είναι ελαφρώς περιστραμμένο σε σχέση με εκείνο μιας άλλης περιοχής χωρίς τη βαρυτική ανωμαλία. Δείτε για παράδειγμα το παρακάτω σχήμα. Ο αριστερός ποδηλάτης (σε αντίθεση με το δεξιό) βρίσκεται σε περιοχή βαρυτικής ανωμαλίας και δε χρειάζεται να κάνει πετάλι για να διατηρήσει την ταχύτητά του: η επιτάχυνση της βαρύτητας (και κατά συνέπεια το βάρος του ως δύναμη, πράσινο βέλος) έχει μια οριζόντια συνιστώσα. Έτσι εκείνος βλέπει ότι βρίσκεται στο ίσιωμα αλλά επιταχύνει σα να βρίσκεται σε κατηφόρα.

Ο αριστερός ποδηλάτης βρίσκεται σε περιοχή βαρυτικής ανωμαλίας και μπορεί να επιταχύνει χωρίς να κάνει πετάλι.

Υπάρχει κάποια τέτοια ανωμαλία στην Πεντέλη και μάλιστα τόσο ισχυρή ώστε να μετατρέψει μια ανηφόρα σε κατηφόρα και το αντίστροφο; Η μήπως αυτό που βλέπουμε στις παραπάνω φωτογραφίες είναι μια οπτική απάτη και τελικά ο δρόμος είναι κατηφορικός, έστω και με ελαφρά κλίση; Θα μπορούσε κάποιος να πει το εξής: αφού θέλουμε να δούμε αν ο δρόμος είναι ανηφορικός ή κατηφορικός, ας βάλουμε στο δρόμο ένα αλφάδι και θα το διαπιστώσουμε αμέσως. Αυτή όμως η προσέγγιση είναι λανθασμένη: οποιαδήποτε βαρυτική ανωμαλία θα επηρεάσει και το ίδιο το αλφάδι με αποτέλεσμα να μη μπορέσουμε να καταλήξουμε σε συμπέρασμα. Για παράδειγμα, αν ο δεξιός ποδηλάτης χρησιμοποιούσε αλφάδι θα συμπέραινε ότι βρίσκεται σε ίσιωμα, ενώ ο αριστερός θα συμπέραινε ότι βρίσκεται σε κατηφόρα. Στην πραγματικότητα όμως, είναι και οι δύο στο ίσιωμα αλλά ο αριστερός είναι σε περιοχή βαρυτικής ανωμαλίας.

Για να διαπιστώσουμε αν ο δρόμος είναι ανηφορικός ή κατηφορικός, χρειαζόμαστε λοιπόν έναν τρόπο ο οποίος να μη χρησιμοποιεί τη βαρύτητα για να ορίσει την κατακόρυφη. Μία λύση θα ήταν να χρησιμοποιήσουμε ένα τοπογραφικό GPS με ακρίβεια μικρότερη του μέτρου. Εφ' όσον όμως δε διαθέτουμε κάτι τέτοιο, θα προσπαθήσουμε να δουλέψουμε με ένα απλό πεζοπορικό GPS. Θα χρησιμοποιήσουμε τη μέθοδο επεξεργασίας των δεδομένων που περιγράψαμε αναλυτικά στην προηγούμενη ανάρτηση. Θα αναφέρουμε κι εδώ κάποια βασικά στοιχεία της μεθόδου, αλλά οι λεπτομέρειες βρίσκονται όλες στην προηγούμενη ανάρτηση, στην οποία εφαρμόσαμε (επιτυχώς) τη μέθοδο για να επαληθεύσουμε ότι ένας δρόμος της γειτονιάς μου είναι πραγματικά ανηφορικός (από όσο γνωρίζω στην περιοχή δεν έχουμε βαρυτικές ανωμαλίες...).

Ξεκινάμε από το σημείο που πήραμε τις φωτογραφίες και αφήνουμε να μας πάρει η "ανηφόρα". Η ανάβαση χωρίς πετάλι συνεχίζεται για περίπου 270 μέτρα και σε κάποιο σημείο σταματά. Ο δρόμος κάνει μια δεξιά στροφή και γίνεται πλέον φανερά ανηφορικός. Το σημείο όπου σταματά η χωρίς πετάλι ανάβαση ας το πούμε Α (έχει γεωγραφικό πλάτος φΑ και γεωγραφικό μήκος λΑ). Είναι το σημείο το οποίο σημειώνεται ως ΤΕLOS στον χάρτη του Google Earth που δείξαμε προηγουμένως. Τώρα ξεκινάμε από το Α και πηγαίνουμε στο σημείο όπου πήραμε τις φωτογραφίες (ας το πούμε Β, σημειώνεται ως ΑΡΧΗ στο χάρτη). Μετά επιστρέφουμε στο Α, κάνουμε αναστροφή και πηγαίνουμε ξανά στο Β, και ξανά στο Α... Κάνουμε αυτό το πηγαινέλα 21 φορές συνολικά. Κατά τη διάρκεια της διαδρομής αυτής το GPS καταγράφει τη θέση (γεωγραφικό πλάτος φ και γεωγραφικό μήκος λ) και το υψόμετρο. Αρχικά ας δούμε πως μεταβάλλεται η απόσταση από το σημείο Α. Ως μέτρο της απόστασης χρησιμοποιούμε την ποσότητα:

 Η γραφική παράσταση του d φαίνεται στο παρακάτω σχήμα.

Η γραφική παράσταστη δεν είναι κάτι περισσότερο από αυτό που αναμέναμε: η απόσταση από το Α είναι αρχικά ελάχιστη, στη συνέχεια αυξάνεται προς μια μέγιστη τιμή, επιστρέφει στην ελάχιστη κ.ο.κ. για όσες φορές διανύσαμε τη διαδρομή. Η συνάρτηση d(t) έχει μια σχεδόν περιοδικότητα. Ποιά είναι η αντίστοιχη γραφική παράσταση που παίρνουμε για το υψόμετρο h(t); Αυτή φαίνεται στο παρακάτω σχήμα.

Μέσα στην καμπύλη αυτή h(t) κρύβεται μια περιοδικότητα όπως εκείνη της γραφικής παράστασης d(t) αλλά είμαι κρυμένη πίσω από ένα "υπόβαθρο" το οποίο συνοδεύει πάντα τις μετρήσεις του υψομέτρου (βλ. την αντίστοιχη ανάρτηση όπου μελετήθηκε το φαινόμενο αυτό). Για να αποκαλύψουμε την κρυμένη αυτή περιοδικότητα και να τη συσχετίσουμε με εκείνη της απόστασης d, μπορούμε να χρησιμοποιήσουμε δύο διαδικασίες. O μία διαδικασία είναι να προσεγγίσουμε το υπόβαθρο με μια ομαλοποίηση (smoothing) της καμπύλης h(t). Ο δεύτερη διαδικασία είναι να αναλύσουμε κατά Fourier την h(t) και να αποκόψουμε τις (περισσότερες από τις) συχνότητες που αντιστοιχούν στο υπόβαθρο. Ας δούμε τα αποτελέσματα καθεμιάς διαδικασίας ξεχωριστά.

Διαδικασία 1: Ομαλοποίηση (smoothing) της καμπύλης h(t)
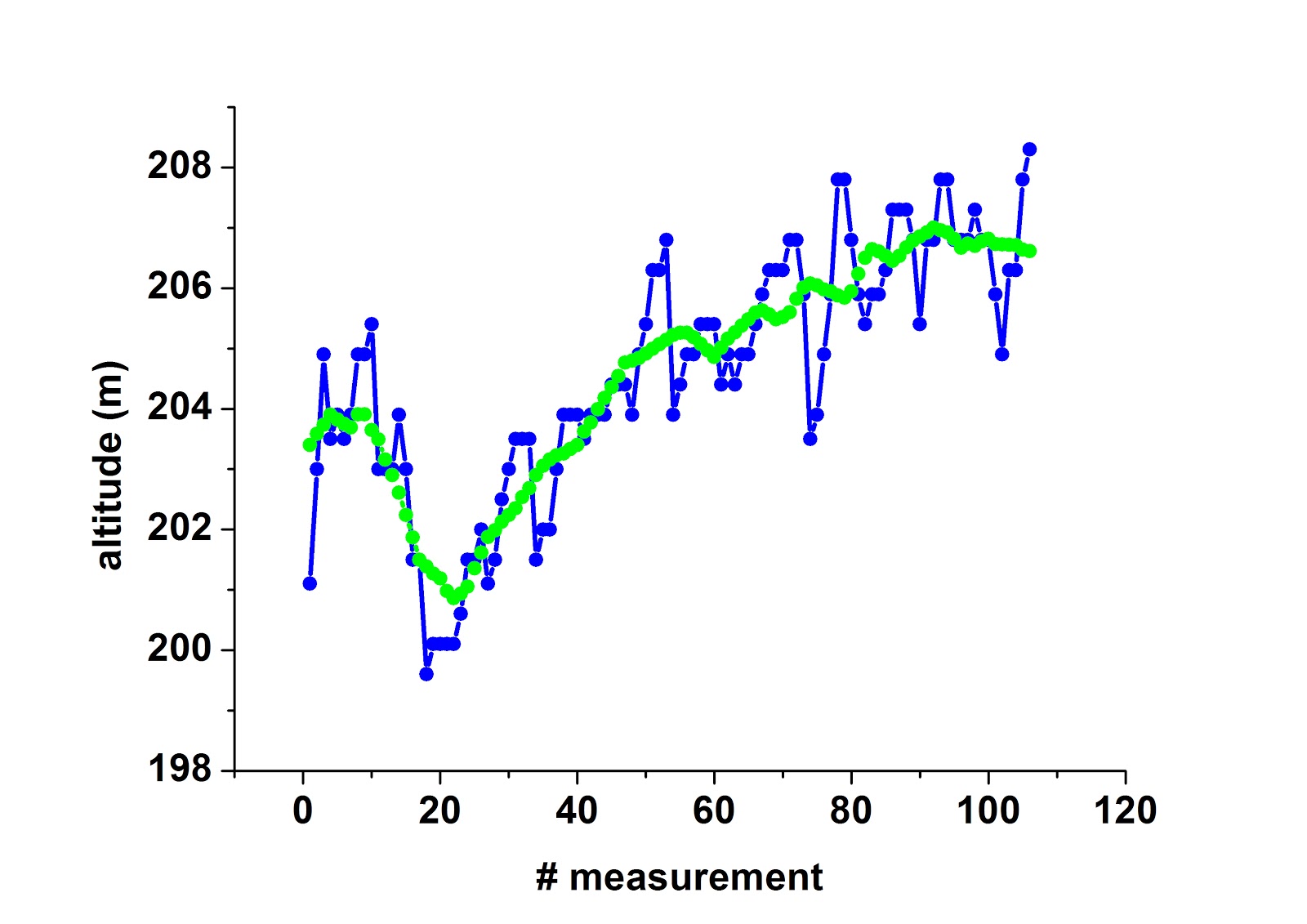
Ένας τρόπος να προσεγγίσουμε το υπόβαθρο της καμπύλης (το ονομάζουμε hB), είναι να την ομαλοποιήσουμε, λαμβάνοντας ως υψόμετρο κάθε σημείου τη μέση τιμή που δίνει ένα πλήθος από γειτονικά σημεία. Το αποτέλεσμα της ομαλοποίησης φαίνεται στο ακόλουθο σχήμα (είναι η πράσινη καμπύλη).

Θεωρώντας ότι το υπόβαθρο hB(t) προσεγγίζεται από την ομαλοποιημένη (πράσινη) καμπύλη, η διαφορά h(t)-hB(t) είναι το υψόμετρο χωρίς το υπόβαθρο. Η γραφική παράσταση του h(t)-hB(t) (δηλαδή μπλέ καμπύλη μείον πράσινη καμπύλη) φαίνεται στο ακόλουθο σχήμα.

Τώρα μένει να συσχετίσουμε τις μεταβολές της απόστασης d με το υψόμετρο χωρίς υπόβαθρο h-hB. Ένας απλός τρόπος να το κάνουμε είναι κάνουμε παραστήσουμε τα σημεία d και h-hB στο επίπεδο και να κάνουμε προσαρμογή (fit) με μια ευθεία ελαχίστων τετραγώνων. Τα αποτελέσματα φαίνονται στο ακόλουθο σχήμα.

Τα αποτελέσματα, οπτικά τουλάχιστο, είναι πολύ καθαρότερα σε σχέση με εκείνα που είχαμε στην προηγούμενη ανάρτηση μελετώντας την κλίση του δρόμου της γειτονιάς μου. Η κλίση της ευθείας είναι αναμφίβολα θετική και υπολογίζεται στην τιμή 1605.72715 με ένα σφάλμα 65.63199. Τι σημαίνει το παραπάνω: όσο αυξάνεται η απόσταση από το σημείο Α (το σημείο που σημειώνεται ως "TELOS" της "βαρυτικής ανηφόρας" στο χάρτη) αυξάνεται το υψόμετρο, δηλαδή το τμήμα του δρόμου που μελετήσαμε είναι ανηφορικό από Πεντέλη προς Νέα Μάκρη και κατηφορικό στην αντίθετη διαδρομή. Αυτό σημαίνει ότι δεν υπάρχει καμία βαρυτική ανωμαλία που να μας ωθεί προς τα πάνω. Αυτό που μας ωθεί είναι η συνιστώσα του βάρους κατά τη διεύθυνση της κίνησής μας σε έναν ελαφρά κατηφορικό δρόμο! Αν υπήρχε βαρυτική ανωμαλία η κλίση της ευθείας θα ήταν αρνητική.

Το αποτέλεσμα του συσχετισμού θέσης d και υψομέτρου h-hB μπορούμε επίσης να το ποσοτικοποιήσουμε υπολογίζοντας το συντελεστή συσχέτισης των δύο αυτών μεγεθών. Το αποτέλεσμα είναι 0.8438. Το θετικό πρόσημο του συντελεστή και η μεγάλη τιμή του (η μέγιστη τιμή του είναι η μονάδα) μας οδηγεί ξανά στο ίδιο συμπέρασμα: απόσταση d και υψόμετρο h-hB είναι θετικά συσχετισμένα, δηλαδή αυξανομένης της απόστασης από το σημείο Α αυξάνεται το υψόμετρο.

Διαδικασία 2: μετασχηματισμός Fourier και ανάλυση συχνοτήτων
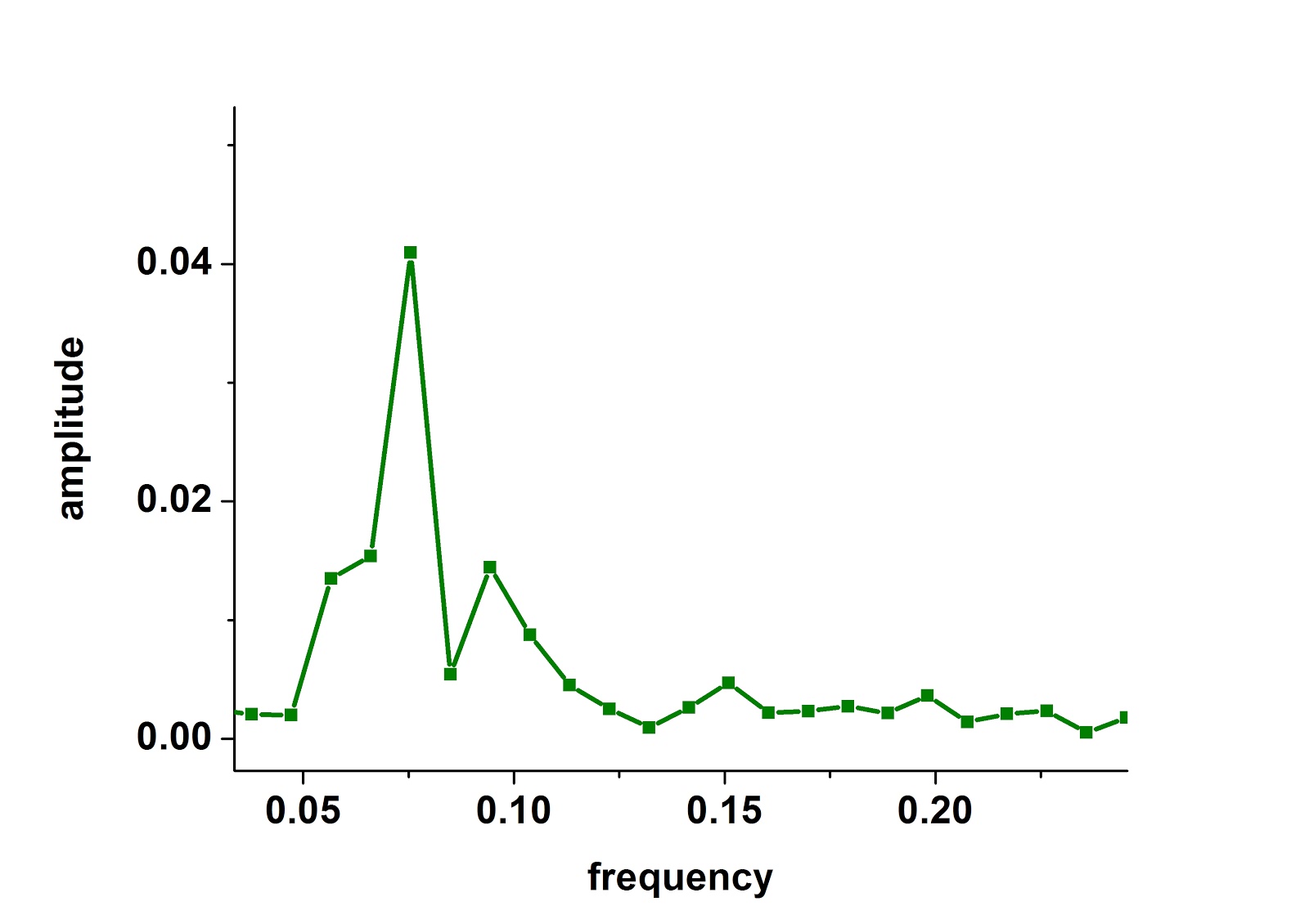
Τα αποτελέσματα της διαδικασίας 1 είναι ολοκάθαρα. Παρόλα αυτά, για λόγους πληρότητας, ας εφαρμόσουμε και τη μέθοδο αυτή για να επιβεβαιώσουμε τα αποτελέσματά μας. Αρχικά λοιπόν κάνουμε ένα μετασχηματισμό Fourier στην καμπύλη d(t). Το αποτέλεσμα για το πλάτος φαίνεται στο ακόλουθο σχήμα.

Η εμφανής κορυφή αντιστοιχεί στη σχεδόν περιοδικότητα της καμπύλης d(t). Οι συχνότητες που αντιστοιχούν στη μεταβολή της καμπύλης d(t) βρίσκονται περίπου μεταξύ των τιμών f1=0.05738 και f2=0.15984. Στη συνέχεια, μετασχηματίζουμε κατά Fourier την καμπύλη του υψομέτρου h(t). Στο μετασχηματισμένο υψόμετρο στο χώρο των συχνοτήτων, κρατάμε μόνο ότι υπάρχει μεταξύ των f1 και f2 και αντιστρέφουμε το μετασχηματισμό. Αυτό που προκύπτει είναι κάτι σαν το h-hB με τη διαφορά ότι ενδέχεται να περιέχει κι άλλες συχνότητες που αντιστοιχούν στο υπόβαθρο. Επειδή όμως το υπόβαθρο είναι καταφανώς μη περιοδικό, θα έχει συνεχές φάσμα και η συνεισφορά του στο επίμαχο διάστημα συχνοτήτων θα είμαι μικρή. Το αποτέλεσμα λοιπόν που παίρνουμε αντιστρέφοντας το μετασχηματισμό (ας το πούμε h1) φαίνεται στο ακόλουθο σχήμα.

Το σήμα που εικονίζεται παραπάνω μπορούμε να το επεξεργαστούμε όπως το h-hB στην προηγούμενη διαδικασία. Παριστώντας τα σημεία στο επίπεδο d - h1 και κάνοντας προσαρμογή με ευθεία ελαχίστων τετραγώνων παίρνουμε το αποτέλεσμα που εικονίζεται στο ακόλουθο σχήμα.

Τα αποτελέσματα είναι και πάλι καθαρά: η κλίση της ευθείας είναι θετική και επομένως τα μεγέθη d και h1 είναι θετικά συσχετισμένα. Η κλίση υπολογίζεται στην τιμή 1281.19 με ένα σφάλμα 65.29. Το θετικό συσχετισμό των d και h1 μπορούμε να τον διαπιστώσουμε και με τον υπολογισμό του συντελεστή συσχέτισης: αυτός υπολογίζεται στην τιμή 0.7836. Η τιμή αυτή υποδηλώνει έντονο θετικό συσχετισμό των μεγεθών.

Ανακεφαλαιώνοντας λοιπόν καταλήγουμε (με δύο μεθόδους επεξεργασίας του σήματος του GPS) στο ασφαλές συμπέρασμα ότι το τμήμα του δρόμου που μελετήσαμε είναι ανηφορικό από Παλαιά Πεντέλη προς Νέα Μάκρη και κατηφορικό από Νέα Μάκρη προς Πεντέλη. Επομένως, δε υπάρχει καμία βαρυτική ανωμαλία που έχει ως αποτέλεσμα να μας "παίρνει η ανηφόρα" από το σημείο που πήραμε τις φωτογραφίες που φαίνονται στην αρχή της ανάρτησης. Ο δρόμος είναι -έστω και ελαφρά- κατηφορικός και τα μάτια μας μας ξεγελούν. Το φαινόμενο οφείλεται καθαρά σε οπτική απάτη. Για την οπτική απάτη πιθανότατα ευθύνεται η κλίση της πλαγιάς στα δεξιά ή/και διαγράμμιση του δρόμου. Επιπλέον πιθανώς σε αυτό να συμβάλλει και το γεγονός ότι στο τέλος υπάρχει πράγματι ανηφόρα (παρατηρήστε το δρόμο στο βάθος που ανεβαίνει καθώς στρίβει δεξιά) που "προκαταλαμβάνει" τον εγκέφαλό μας, ο οποίος εύκολα μπορεί να εξαπατηθεί, όπως φαίνεται στο παρακάτω σχήμα.

Δεν είναι καθόλου δύσκολο να εξαπατήσουμε τον εγκέφαλό μας: οι γραμμές είναι παράλληλες αλλά φαίνονται να σχηματίζουν γωνία (πηγή: http://www.scopper.co.uk/optical/pages/lines_gif.htm)

Παρακάτω φαίνονται κάποιες επιπλέον φωτογραφίες από την εξόρμηση που κάναμε για τη λήψη των μετρήσεων.

Πειράματα με ένα GPS, μέρος ΙΙ: ανηφόρες και κατηφόρες

Στην προηγούμενη ανάρτηση αυτής της "τριλογίας" διαπιστώσαμε ότι δε μπορούμε να επαυξήσουμε την ακρίβεια ενός απλού πεζοπορικού GPS (τυπικά έχει ακρίβεια ως 4-5 μέτρα) παίρνοντας πολλαπλές μετρήσεις και κάνοντας στατιστική επεξεργασία. Τα αποτελέσματα της καταγραφής δεν είναι απλώς σημεία που ακολουθούν μια κατανομή γύρω από μια μέση τιμή παρά εμφανίζουν μεταβολές που εκτείνονται σε μεγάλη χρονική κλίμακα. Το πρόβλημα όμως που μας οδήγησε στους πειραματισμούς της προηγούμενης ανάρτησης παραμένει: πως μπορούμε να διαπιστώσουμε αν ένας δρόμος είναι ανηφορικός ή κατηφορικός χρησιμοποιώντας ένα τέτοιο GPS; Υπάρχει κάποιος τρόπος να επιβεβαιώσουμε ή να καταρρίψουμε το θρύλο της "βαρυτικής ανηφόρας" της Πεντέλης;

Η απάντηση είναι ότι πιθανότατα υπάρχει, αλλά θα χρειαστεί να κάνουμε αρκετή ανάλυση στα δεδομένα του GPS. Πριν πάρουμε τα βουνά προς αναζήτηση της "βαρυτικής ανηφόρας", θα κάνουμε ένα αντίστοιχο πείραμα σε ένα δρόμο της γειτονιάς για να δούμε αν η μέθοδός μας δουλεύει. To τμήμα του δρόμου που θα ελέγξουμε ξεκινά από ένα σημείο Α και καταλήγει σε ένα σημείο Β τα οποία απέχουν μεταξύ τους 215 μέτρα. Ξέρουμε ότι το σημείο Β είναι υψομετρικά ψηλότερα (περίπου 4-5 μέτρα). Θα μπορέσουμε με μια κατάλληλη επεξεργασία του σήματος του GPS να το διαπιστώσουμε και πειραματικά;

Ξεκινάμε λοιπόν, με το GPS στο χέρι, να διανύουμε την απόσταση από το ένα σημείο στο άλλο πολλές φορές. Κατά τη διάρκεια της διαδρομής μας καταγράφουμε με το GPS τη θέση (γεωγραφικό πλάτος φ και γεωγραφικό μήκος λ) και το υψόμετρο. Σε όλο το μήκος της διαδρομής η λήψη του σήματος είναι πολύ καλή και ο δέκτης έχει τη μέγιστή του ακρίβεια. Αφού διανύσουμε την απόσταση Α-Β 15 φορές, "κατεβάζουμε" τα δεδομένα του GPS και κάνουμε αρχικά δύο γραφικές παραστάσεις: της απόστασης από το σημείο Α και του υψομέτρου, οι οποίες φαίνονται στα παρακάτω σχήματα.
Τεχνικές λεπτομέρειες: η πρώτη γραφική παράσταση, στον κατακόρυφο άξονα δεν έχει ακριβώς την απόσταση αλλά ένα μέτρο αυτής, συγκεκριμένα το άθροισμα των τετραγώνων των διαφορών γεωγραφικού μήκους και πλάτους από το σημείο Α. Επίσης στον οριζόντιο άξονα δεν είναι ο χρόνος αλλά ο αριθμός της μέτρησης.

Με βάση αυτά που διαπιστώσαμε στην προηγούμενη ανάρτηση, τα αποτελέσματα δε μας εκπλήσσουν. Η πρώτη γραφική παράσταση παρουσιάζει ταλαντωτική συμπεριφορά με πολύ λίγες διακυμάνσεις, καθώς η διανυόμενη απόσταση (~215 μέτρα) είναι πολύ μεγαλύτερη από την ακρίβεια της συσκευής (~4-5 μέτρα). Η δεύτερη γραφική παράσταση μοιάζει σε πρώτη ανάγνωση απογοητευτική. Κανονικά θα περιμέναμε να παρουσιάζει κι εκείνη μια ταλαντωτική συμπεριφορά απόλυτα συσχετισμένη με εκείνη της πρώτης. Αυτή η ταλαντωτική συμπεριφορά υπάρχει αλλά είναι κρυμμένη πίσω από ένα υπόβαθρο μεγάλων μεταβολών της καταγραφής του υψομέτρου σαν κι εκείνο που είδαμε στην προηγούμενη ανάρτηση. Το ζήτημα επομένως ανάγεται στο εξής: μπορούμε με κάποιον τρόπο να δούμε την ταλάντωση που είναι κρυμμένη πίσω από το υπόβαθρο των μετρήσεων του υψομέτρου και να τη συσχετίσουμε με την ταλάντωση της θέσης;

Υπάρχουν δύο διαδικασίες επεξεργασίας για να αποκαλύψουμε αυτή την ταλάντωση, η πρώτη είναι πιο απλή και εύκολη υπολογιστικά ενώ η δεύτερη απαιτεί κάποιους περισσότερους υπολογισμούς.

Διαδικασία 1: ομαλοποίηση (smoothing) της καμπύλης του υψομέτρου

Για να προσεγγίσουμε το υπόβαθρο το οποίο μας κρύβει την ταλάντωση, μπορούμε να υποθέσουμε πως αυτό ακολουθεί κατά κάποιο τρόπο τη μέση τιμή της καμπύλης. Κάνουμε λοιπόν ομαλοποίηση (smoothing) της καμπύλης λαμβάνοντας για κάθε σημείο, τη μέση τιμή που δίνουν τα γειτονικά του σημεία. Το αποτέλεσμα της ομαλοποίησης φαίνεται στο ακόλουθο σχήμα (πράσινη καμπύλη).

Υποθέτοντας ότι το υπόβαθρο είναι η πράσινη (ομαλοποιημένη) καμπύλη, η ταλάντωση κρύβεται στη διαφορά μεταξύ των μετρήσεων υψομέτρου (μπλέ καμπύλη) και στο υπόβαθρο (πράσινη καμπύλη). Η διαφορά αυτή φαίνεται στο ακόλουθο σχήμα (με h συμβολίζουμε το υψόμετρο και με hB το υπόβαθρο).

 Υπάρχει μια ταλαντωτική συμπεριφορά που δεν παρουσιάζει την ομαλότητα της καμπύλης της απόστασης αλλά ας προσπαθήσουμε τώρα να συσχετίσουμε το μέγεθος h - hB με την απόσταση. Υπάρχουν δύο τρόποι να γίνει αυτός ο συσχετισμός:

Τρόπος 1: Υπολογισμός της κλίσης της ευθείας ελαχίστων τετραγώνων
Ο δρόμος που μελετάμε έχει σχεδόν σταθερή κλίση, επομένως η γραφική παράσταση h - hB σα συνάρτηση της απόστασης θα έπρεπε να ακολουθεί μια ευθεία. Αν η ευθεία έχει θετική κλίση τότε έχουμε ανηφόρα, αν έχει αρνητική τότε έχουμε κατηφόρα. Ας δούμε λοιπόν πως μοιάζουν τα σημεία μας στο επίπεδο όπου οριζόντιος άξονας είναι η απόσταση και κατακόρυφος η διαφορά h - hB.

 Δεν πολυμοιάζουν να ακολουθούν ευθεία αλλά ας κάνουμε μια προσαρμογή μιας ευθείας με τη μέθοδο των ελαχίστων τετραγώνων. Το αποτέλεσμα μας δίνει για την κλίση της τιμή 268.02841 με σφάλμα ίσο με 127.50361. Το σφάλμα είναι μεγάλο (όπως αναμένονταν δεδομένης της διασποράς των σημείων) αλλά είναι μικρότερο από την κλίση, επομένως μπορούμε με ασφάλεια να πούμε ότι από το Α στο Β έχουμε ανηφόρα. Και πράγματι έτσι είναι: ο δρόμος που μελετήσαμε είναι και δείχνει ανηφόρα!

 Τρόπος 2: Υπολογισμός του συντελεστή συσχέτισης του Pearson
Ένα μέγεθος το οποίο μπορεί να ποσοτικοποιήσει τη συσχέτιση δύο μεγεθών είναι ο συντελεστής συσχέτισης του Pearson. Αυτός είναι ένα μέτρο του κατά πόσο δύο μεταβλητές (ας τις πούμε x και y) μεταβάλλονται μαζί. Θετικός συντελεστής συσχέτισης σημαίνει ότι όσο αυξάνεται η μία μεταβλητή αυξάνεται και η άλλη. Αρνητικός συντελεστής συσχέτισης σημαίνει ότι όσο αυξάνεται η μία μεταβλητή μειώνεται η άλλη. Όσο πιο μεγάλη είναι η απόλυτη τιμή του συντελεστή συσχέτισης τόσο πιο ισχυρή είναι η συσχέτιση των δύο μεταβλητών x και y. Ο συντελεστής συσχέτισης ορίζεται από τον τύπο:

όπου το < > υποδηλώνει τη μέση τιμή. Αν η σχέση των x και y είναι γραμμική (πχ y=ax), ο συντελεστής παίρνει τη μέγιστη απόλυτη τιμή του που είναι η μονάδα: r = 1 αν a>0 και r = -1 αν a<0. Ας εξετάσουμε λοιπόν κατά πόσο είναι συσχετισμένα τα μεγέθη της απόστασης και της διαφοράς υψομέτρου h - hB. Το αποτέλεσμα είναι r = 0.2353, δηλαδή τα μεγέθη είναι θετικά συσχετισμένα: αυξάνομένης της απόστασης από το Α, αυξάνεται και το υψόμετρο. Βρήκαμε λοιπόν και πάλι ότι έχουμε ανηφόρα! 

Πριν καταλήξουμε οριστικά στο συμπέρασμα ότι έχουμε ανηφόρα καλό είναι να συγκρίνουμε το συντελεστή αυτόν που υπολογίσαμε με εκείνον της συσχέτισης κάποιων άλλων μεγεθών. Έτσι, υπολογίζουμε επιπλέον τη συσχέτιση της απόστασης με δύο ακόμα μεγέθη: το υψόμετρο όπως το παίρνουμε από το GPS χωρίς κανένα μετασχηματισμό καθώς και μια τεχνητή σειρά δεδομένων που αποτελείται από τυχαίους αριθμούς. Τα αποτελέσματα είναι αντίστοιχα r = 0.07135 και r = 0.05328. Και τα δύο είναι πολύ μικρότερα από την τιμή 0.2353, κάτι που υποδηλώνει ότι η θετική συσχέτιση της απόστασης με το h - hB δεν είναι κάποιο τυχαίο γεγονός.

Διαδικασία 2: μετασχηματισμός Fourier και φιλτράρισμα συχνοτήτων

Μέσα στην καμπύλη του υψομέτρου όπως την παίρνουμε από το GPS (η μπλέ καμπύλη που είδαμε στο δεύτερο σχήμα) είναι κρυμμένη μια περιοδικότητα στη μεταβολή του υψομέτρου. Η περιοδικότητα αυτή έχει κάποια συχνότητα (ή ακριβέστερα ένα φάσμα συχνοτήτων) την οποία μπορούμε να βρούμε εύκολα κοιτώντας την καμπύλη της απόστασης (την πρώτη κόκκινη καμπύλη). Είναι φανερό ότι η καμπύλη αυτή έχει μια περιοδικότητα. Επειδή το υψόμετρο μεταβάλλεται μονότονα με την απόσταση, την ίδια περιοδικότητα θα έχει και η μεταβολή του υψομέτρου. Αυτή είναι η κρυμμένη περιοδικότητα που ψάχνουμε. Το σκεπτικό λοιπόν είναι να βρούμε το φάσμα συχνοτήτων της απόστασης και από τις συχνότητες που συναποτελούν την καμπύλη του υψομέτρου και να εστιαστούμε σε εκείνες που μας ενδιαφέρουν. Παρακάτω περιγράφουμε πιο αναλυτικά τη μέθοδο.

Ας συμβολίσουμε με h(t) την καμπύλη υψομέτρου που παίρνουμε από το GPS και με s(t) την αντίστοιχη καμπύλη "απόστασης" (τεχνική λεπτομέρεια: η έννοια του χρόνου t χρησιμοποιείται κάπως καταχρηστικά, καθώς όπως είπαμε στον οριζόντιο άξονα είναι ο αριθμός της μέτρησης και οι μετρήσεις δεν είναι ακριβώς ισόχρονες). Για να βούμε το φάσμα των συχνοτήτων της s(t) θα κάνουμε ένα μετασχηματισμό Fourier:

 Το πλάτος του μετασχηματισμού (το μέτρο του μιγαδικού S(f)) φαίνεται στο ακόλουθο σχήμα.

 Όπως αναμένονταν από την εμφανή περιοδικότητα της s(t), το πλάτος είναι κυρίως συγκεντρωμένο σε μια περιοχή συχνοτήτων μεταξύ των τιμών f1=0.0471 και f2=0.132. Η ιδέα τώρα είναι να "κρατήσουμε" από την h(t) ότι υπάρχει μέσα σε αυτό το εύρος συχνοτήτων πετώντας όλα τα υπόλοιπα και αυτό γίνεται ως εξής:

1) Υπολογίζουμε το μετασχηματισμό Fourier της h(t):

2) Από όλες τις συχνότητες που περιέχει η H(f) κρατάμε μόνο εκείνες που βρίσκονται μεταξύ των f1 και f2. Πιθανότατα βέβαια στο διάστημα αυτό των συχνοτήτων, εκτός από την περιοδικότητα της μεταβολής του υψομέτρου, να υπάρχει και κάποιο μικρό πλάτος που οφείλεται σε μεταβολές του σήματος του GPS. Ουσιαστικά, φιλτράρουμε την H(f) και δημιουργούμε μια καινούργια H(f) που περιέχει συνεισφορές μόνο από το συγκεκριμένο διάστημα συχνοτήτων:

 3) Για να βρούμε το μέρος της h(t) που αντιστοιχεί στο διάστημα αυτό των συχνοτήτων, εφαρμόζουμε τον αντίστροφο μετασχηματισμό Fourier σε αυτή την καινούργια H(f), και παίρνουμε μια συνάρτηση h1(t) που εμπεριέχει την περιοδικότητα στη μεταβολή του υψομέτρου:

 Το αποτέλεσμα h1(t) που προκύπτει από τα 3 παραπάνω βήματα φαίνεται στο παρακάτω σχήμα:

 Τώρα λοιπόν, θα συσχετίσουμε το παραπάνω h1(t) με το s(t) με τους δύο τρόπους που είδαμε προηγουμένως:

Υπολογίζοντας την κλίση της ευθείας ελαχίστων τετραγώνων στο επίπεδο s - h1 παίρνουμε την τιμή  246.17802 για την κλίση και την τιμή 88.70148 για το σφάλμα της. Και πάλι λοιπόν καταλήγουμε στο αληθές συμπέρασμα ότι ο δρόμος μας είναι πράγματι ανηφορικός από το Α στο Β, και μάλιστα με μικρότερο σχετικά σφάλμα για την κλίση της ευθείας. Στο παρακάτω σχήμα φαίνονται τα σημεία και η βέλτιστη ευθεία με την παραπάνω κλίση.

 Μπορούμε να καταλήξουμε στο ίδιο συμπέρασμα υπολογίζοντας το συντελεστή συσχέτισης των s και h1 και το αποτέλεσμα είναι 0.2624. Τα μεγέθη s και h1 είναι επομένως συσχετισμένα: αυξανομένης της απόστασης από το Α αυξάνεται το υψόμετρο, άρα επαληθεύσαμε και πάλι ότι ο δρόμος είναι ανηφορικός από το Α στο Β.

Συμπερασματικά: Περιγράψαμε μια μέθοδο με την οποία μπορούμε να διαπιστώσουμε αν ένας δρόμος είναι ανηφορικός η κατηφορικός και την ελέγξαμε σε ένα δρόμο του οποίου γνωρίζουμε την κλίση. Η μέθοδος φάνηκε να δουλεύει και σε επόμενη ανάρτηση θα την εφαρμόσουμε σε ένα δρόμο που δεν ξέρουμε αν είναι ανηφορικός ή κατηφορικός: στη "βαρυτική ανηφόρα" της Πεντέλης.